Python Exercises

Yazan:matmuh19Yazı kategorisi Kodlama

Write a python function that returns  for a given real number x.

$2\sin(x^2) + \ln(|x|) + 1$
from math import sin, log
def f(x):
    return 2*sin(x*2) + log(abs(x)) + 1.0
f(1.0)
output : 2.682941969615793

Write a python function that takes

  • A function f(x)
  • A pair of real numbers (a,b)
  • An integer N

as input and returns the Riemann sum of f(x) on the interval [a,b] with N equal subdivisions.

import numpy as np
from math import pi

def RiemannSum(f, interval, N):
    a,b = interval
    dx = (b-a)/N
    xs = np.linspace(a,b,N)
    fv = np.vectorize(f)
    return dx*sum(fv(xs))

RiemannSum(sin,(0,pi),100)
output : 1.9798338422550525
  • Pull 100 uniformly random numbers from the interval $[0,1]$ as an array xs.
  • Add 0 at the beginning of the array, and 1.0 at the end.
  • Sort the array xs from smallest to the largest.
  • Calculate its discrete derivative ys, i.e. let $y_i = x_{i+1} - x_i$
from numpy.random import uniform

xs = np.append(np.array([0.0, 1.0]), uniform(0.0,1.0,100))
xs.sort()
ys = np.diff(xs) 
ys
array([0.01453743, 0.00156663, 0.00534638, 0.00096398, 0.00508993,
       0.00113972, 0.00794464, 0.00759768, 0.01644741, 0.0231801 ,
       0.00176902, 0.004525  , 0.00651795, 0.02118523, 0.00246595,
       0.00211198, 0.00827289, 0.0095773 , 0.01107778, 0.00116672,
       0.00555542, 0.00197661, 0.00577502, 0.00075182, 0.00150462,
       0.03740627, 0.00321144, 0.01643881, 0.00950991, 0.00428141,
       0.00352253, 0.03885483, 0.04457475, 0.00533743, 0.01936863,
       0.00513555, 0.01066424, 0.00294978, 0.00050975, 0.02545816,
       0.00922468, 0.00474569, 0.0266568 , 0.00308083, 0.00432957,
       0.00399059, 0.00019818, 0.00880208, 0.00519906, 0.01766466,
       0.00367313, 0.00523431, 0.011792  , 0.00963488, 0.00749983,
       0.01861325, 0.00230705, 0.01085615, 0.01071165, 0.00674251,
       0.00317664, 0.00183448, 0.01546867, 0.01741572, 0.00078044,
       0.02498636, 0.02380307, 0.00063454, 0.02738756, 0.00156014,
       0.01222296, 0.04473237, 0.00149226, 0.00895459, 0.03045946,
       0.01131244, 0.00189771, 0.02297412, 0.01214312, 0.00028657,
       0.00204055, 0.008042  , 0.00131223, 0.00237684, 0.0159444 ,
       0.01281529, 0.01844092, 0.00610445, 0.00847108, 0.00456424,
       0.0008383 , 0.01559287, 0.01621418, 0.01133397, 0.00506612,
       0.00333   , 0.01781157, 0.0023699 , 0.00521517, 0.00142389,
       0.01094116])

  • Pull 100 uniformly random numbers from the interval $[0,1]$ into an array xs.
  • Pull 100 random numbers from the Gaussion distribution with $\mu=0$ and $\sigma=1.0$ into an array ys.
  • Scatter plot xs against ys using matplotlib
from numpy.random import uniform, normal
from matplotlib.pyplot import scatter

xs = uniform(0.0, 1.0, 100)
ys = normal(0.0, 1.0, 100)

scatter(xs,ys)

output :

Using the numpy library

A = np.random.rand(100,100)
A100 = A**100
eigval, eigvec = np.linalg.eig(A)
u,s,vh = np.linalg.svd(A)
  • Pull the text of a novel by Dickens from the website of Gutenberg Project
  • Remove all non-alphanumeric characters
  • Split the text into words and convert them into lower case
  • Count the number of distinct words in the text
  • Count how many times each word occurs within the text
from urllib.request import urlopen
from collections import Counter
from re import sub

raw = urlopen("https://www.gutenberg.org/files/1400/1400-0.txt")
text = raw.read().decode('utf-8').lower()
processed = sub('[^a-z ]','',text).split()

len(set(processed))
  • Write a python function CountWords that takes the URL for a text and returns the number of unique words within the text.
  • Write a python function Top20Words that takes the URL for a text and returns the most frequently appearing top 20 words within the text.
def CountWords(url):
    raw = urlopen(url)
    text = raw.read().decode('utf-8').lower()
    processed = sub('[^a-z ]','',text).split()
    return len(set(processed))

CountWords('https://www.gutenberg.org/files/1400/1400-0.txt')
output : 23777
def TopNWords(url, N):
    raw = urlopen(url)
    text = raw.read().decode('utf-8').lower()
    processed = sub('[^a-z ]','',text).split()
    res = Counter(processed)
    return sorted(res,key=res.get,reverse=True)[:N]

TopNWords('https://www.gutenberg.org/files/1400/1400-0.txt',20)
output : 
['the',
 'and',
 'i',
 'to',
 'of',
 'a',
 'in',
 'that',
 'was',
 'it',
 'he',
 'you',
 'had',
 'my',
 'me',
 'his',
 'with',
 'as',
 'at',
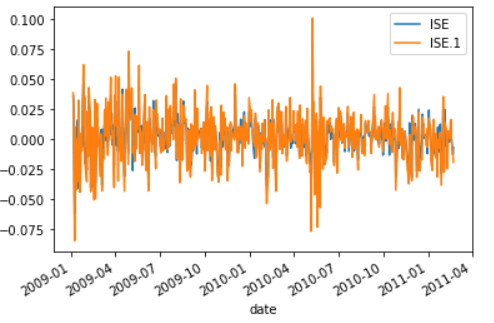
 'said']
  • Pull the IMKB data from UCI using pandas.
  • Plot the TL based ISE and USD based ISE columns together in the same graph.
  • Calculate how many times NIKKEI was higher than FTSE.
import pandas as pd

data = pd.read_excel('https://archive.ics.uci.edu/ml/machine-learning-databases/00247/data_akbilgic.xlsx', header=1)

data.plot('date',['ISE','ISE.1'])
len(data['date'][data['NIKKEI']>data['FTSE']])

Yorum bırakın